Introduction
Using quantum mechanical calculations in order to calculated molecular properties for the discovery of new materials can be a slow and expensive method. By combining those calculations with machine learning methods and genetic algorithms we accelerated the search for nnovel conjugated polymers with optimized properties. In our researche we used machine learning as a screening tool to find polymers with low reorganization energy, as well as used a genetic algorithm to find polymers with a stable triplet ground-state. The semi-empirical method GFN2-xTB was used in both cases as a surrogate to DFT in order to greatly accelerate the search for polymers with these properties.
Marcus Reorganization Energy
Marcus reorganization energy (λ) describe the energy barrier for a hole transfer. Four different calculations are reuiqred to calculate the reoeganization energy of a molecule:
- Energy of the optimized neutral molecule (\(E_0\))
- Energy of the optimized cationic molecule (\(E_+\))
- Energy of the neutral molecule at the cation grometry (\(E_0^*\))
- Energy of the cationic molecule at the neutral geometry (\(E_+^*\))
The reorganization energy is calculated as:
\[\lambda = \lambda~_0 + \lambda~_+ = (E_0^* - E_0) + (E_+^* - E_+)\]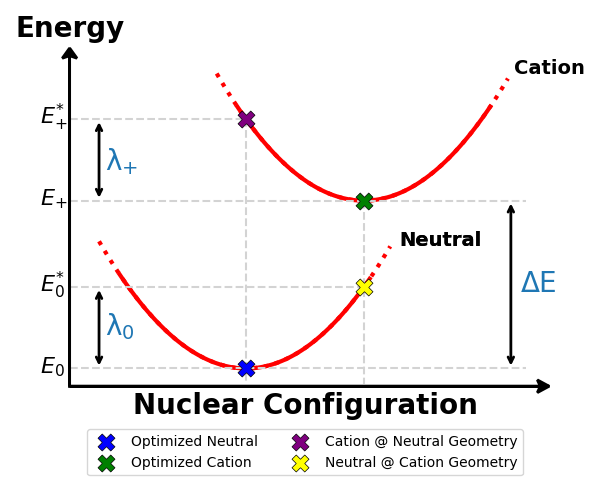
Those calculations can pose a great computational cost which increases exponentially with the number of atoms in the molecule.
Conductive and semiconductive organic polymers with small reorganization energy have many potential uses in various electronic devices, but searching through the vast chemical space to find polymer candidates can be long and computationally expensive. We used machine learning models to predict λ of thiophene-based co-polymers, made from two different monomers from a list of 253 monomers. This gives us 32,131 possible oligomer families.
We used the B3LYP DFT functional to calculate the λ of a small group of oligomers with length of 4 and 6 monomers (tetramers and hexamers, respectively) as a training set for the machine learning models. We used the GFN2-xTB semi-empirical method to calculate various molecular features, such as inter-monomer bond length and angle, as well used RDKit for other features such as ECFP4. Additionally, we also included \(\pi\)-system size feature. We compared five different models and trained them each three times on different splits of the training set.
| Random forest | Neural network | Gradient boosting trees | Ridge regression | Kernel ridge regression | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSE (eV) | R2 | RMSE (eV) | R2 | RMSE (eV) | R2 | RMSE (eV) | R2 | RMSE (eV) | |
| Run 1 | 0.716 | 0.108 | 0.631 | 0.122 | 0.645 | 0.121 | 0.655 | 0.118 | 0.683 | 0.113 |
| Run 2 | 0.662 | 0.118 | 0.653 | 0.120 | 0.575 | 0.134 | 0.644 | 0.121 | 0.680 | 0.115 |
| Run 3 | 0.685 | 0.114 | 0.623 | 0.125 | 0.612 | 0.129 | 0.666 | 0.117 | 0.686 | 0.114 |
| Average | 0.687 | 0.113 | 0.636 | 0.122 | 0.611 | 0.128 | 0.655 | 0.119 | 0.683 | 0.114 |
| ±0.016 | ±0.003 | ±0.009 | ±0.001 | ±0.020 | ±0.004 | ±0.006 | ±0.001 | ±0.002 | ±0.001 | |
The random forest model had the best performance with \(R^2 = 0.687 ± 0.016\) and \(RMSE = 0.113 ± 0.003 eV\). The prediction on the test set shows a heteroscedastic behavior, where the prediction is less accurate for higher λ. However, this model can be used as a screening tool to find oligomers with small λ.
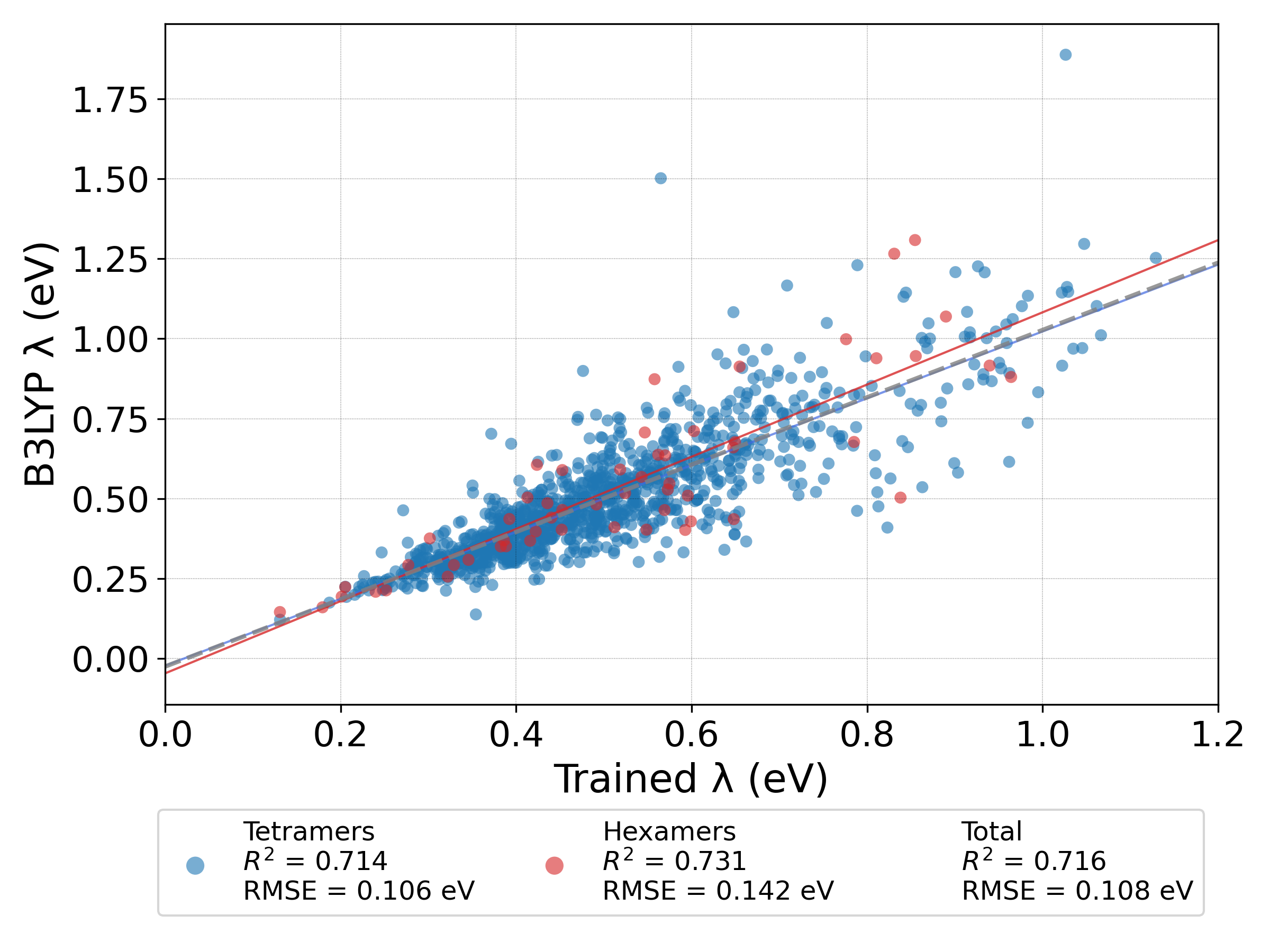
While machine learning model struggle to accuretly predict a large range of reorganization energies, they can still be used to find oligomers with a small λ, which can have better performace in various electronic device. By using machine learning we have accelerated the search for polymers with low λ 13× versus calculating the λ for each polymer using DFT.
The full research paper can be found here: DOI, ChemRxiv (open access). Raw data can be found on GitHub.
Ground-State Triplet
Organic polymers with a triplet ground state, i.e., a biradical with two unpaired electrons, have interesting properties and potential uses. Those polymers are made from pairs of electron-donor and electron-acceptor monomers which lower the HOMO-LUMO gap and stabilize the triplet ground state. We were interested in finding out what are the predicting properties that can help with discovering new biradical polymers. We used the $\omega$~B97X-D3 DFT method to calculate the HOMO-LUMO gap of the singlet and the stability of the triplet species of 132 oligomers created from 12 acceptor and 11 donor monomers. We found a linear correlation between the HOMO-LUMO gap of the singlet species and the stability of the triplet (calculated as the difference between the electronic energies of the triplet and singlet species, \(\Delta E_{T-S}\)), as well as a correlation between the identity of the acceptor monomer and the stability of the triplet ground state.
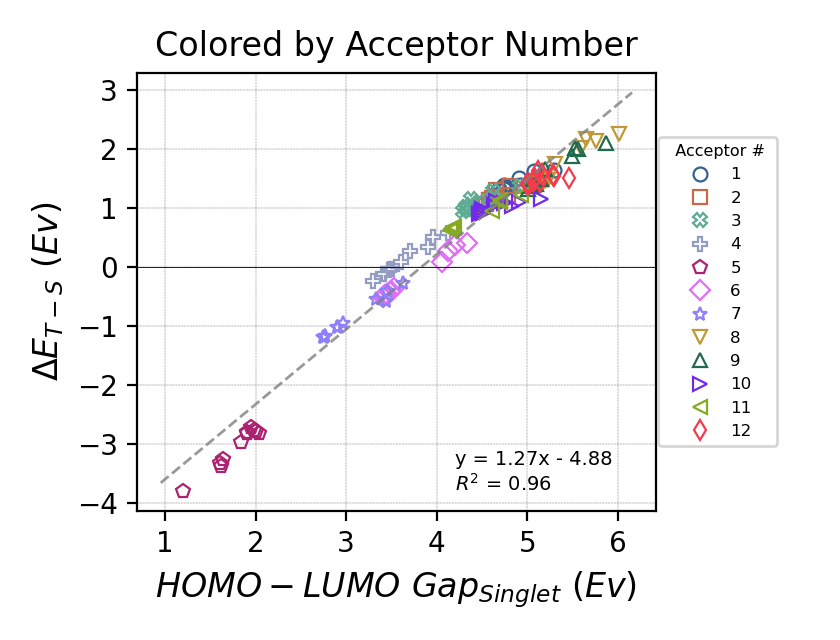
Full research paper can be found here: DOI, ChemRxiv (open access). Raw data can be found on GitHub.
The HOMO-LUMO gap of the singlet species was found to be the best predictor for the stability of the triplet ground state of the oligomer. Additionally, we have found that HOMO-LUMO gap calculated using the semi-empirical GFN2-xTB correlates with the gap calculated using the $\omega$~B97X-D3 DFT method, which can greatly help accelerate the search for new biradical polymers. Therefor, we used a genetic algorithm combined with GFN2-xTB calculations to search for oligomers, created from combining two monomers from a pool of 1226 possible monomers, with a small HOMO-LUMO gap. The number of possible monomer combination is above 1.5 million (\(1226^2\)) which makes running calculations on all of them impractical, which is why a genetic algorithm can help as it combs through the possible monomer combinations more efficiently than an exhaustive search.
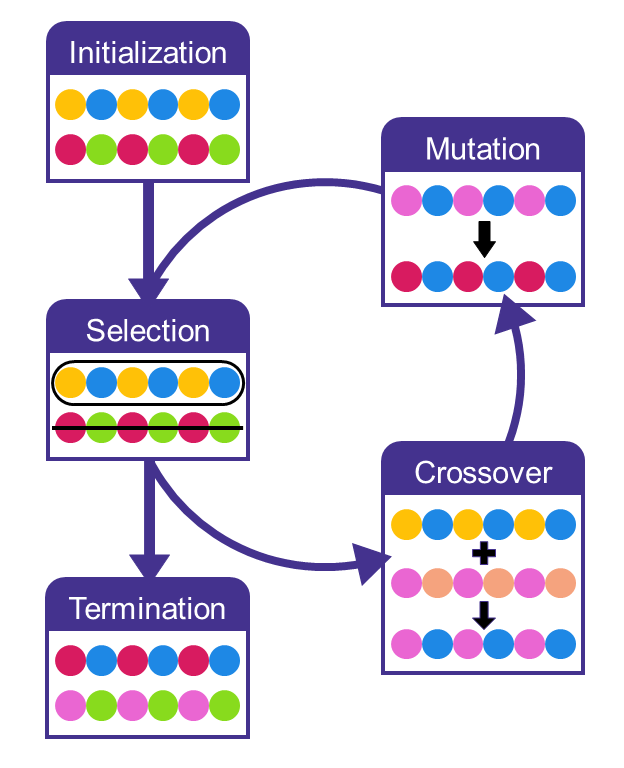
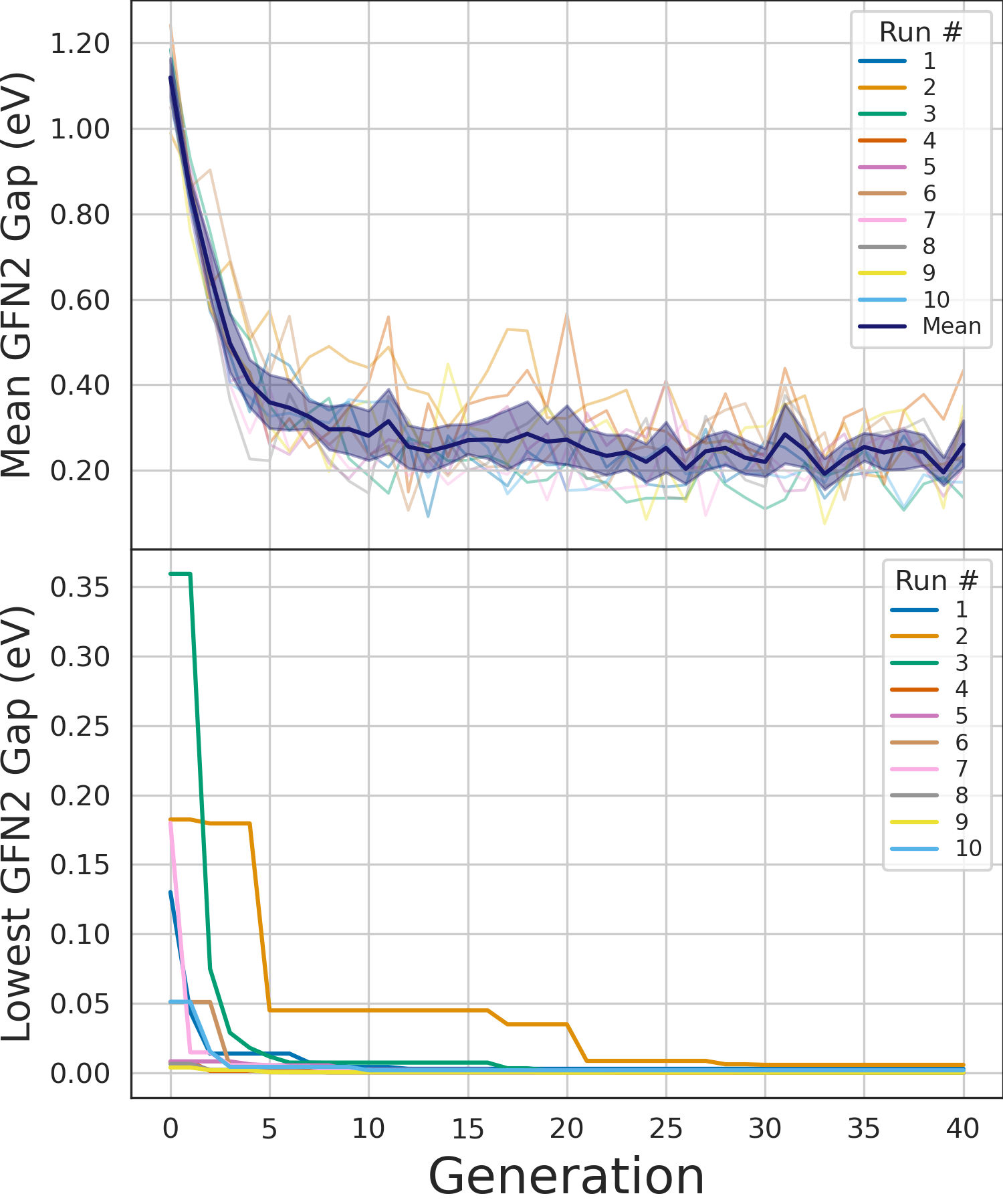
We ran the genetic algorithm ten times to increase the breadth of the search as genetic algorithms are a stochastic optimization method and relies on random chance. The genetic algorithm found new monomer combinations that lead to oligomers with a lower HOMO-LUMO gap with every generation. The algorithm stopped after 40 generations, which were enough to find oligomers with a HOMO-LUMO gap < 0.01 eV.
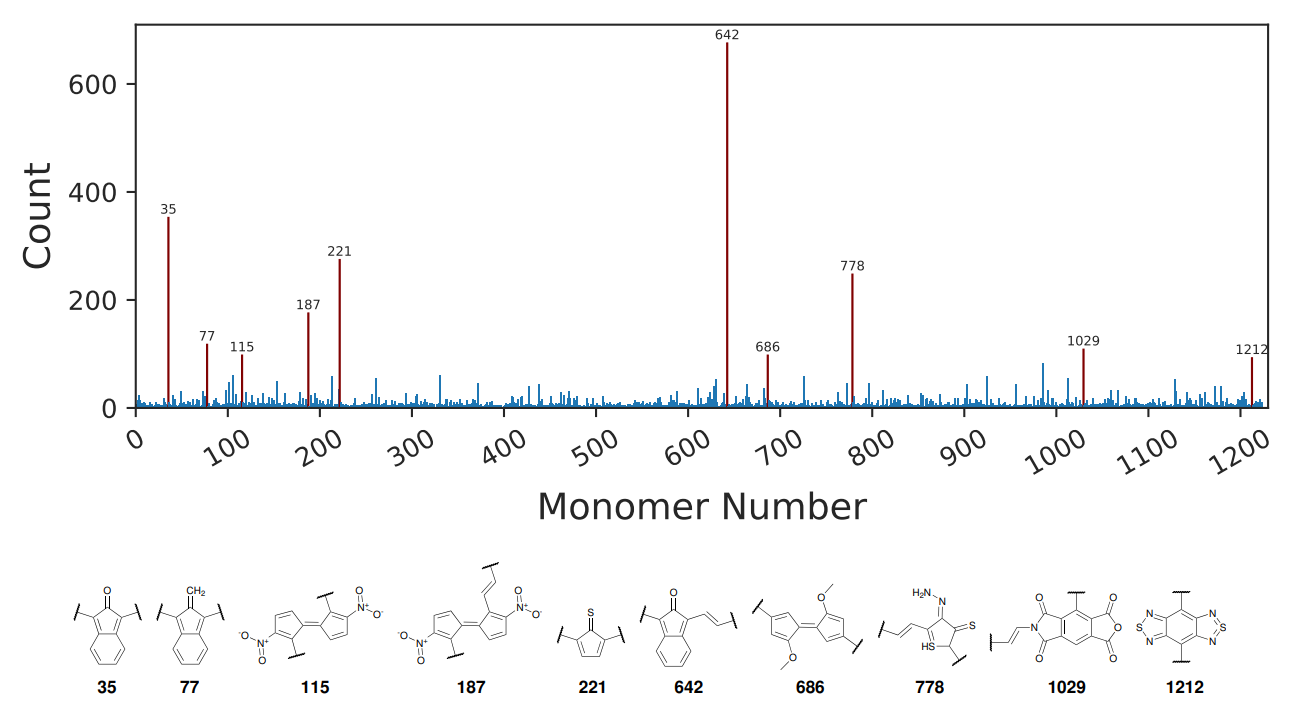
Additionally, we have analyzed the results of the genetic algorithm to see which monomers have been more frequently selected by the algorithm. We have found that there are ten common monomers that promote a low HOMO-LUMO gap. Monomer 642 and 35 are the two most common monomers, and they share a molecular structure where monomer 642 also includes a vinyl bridge group. A vinyl bridge has been shown to lower the HOMO-LUMO gap and we see that this motif is also the only difference between monomers 115 and 187, and it also appears in monomers 778 and 1029.
We have shown that a genetic algorithm, combined with the GFN2-xTB method, can find ground state triplet polymer candidates faster than a exhaustive search, and faster than using DFT methods.
Full paper can be found here: ChemRxiv (open access). Raw data can be found on GitHub.